100 Days Of ML Code — Day 081

Recap From Day 080

Day 080, we looked at loudness and pitch. You can catch up using the link below. 100 Days Of ML Code — Day 080 Recap From Day 079medium.com

Today, we will continue from where we left off in day 080

Loudness Continued

As we’re thinking about frequency, we think about frequency as going up linearly and there’s a key musical construct that’s described. It’s called the Harmonic Series. If we have a base frequency at say 100 Hertz, well we can think of integer multiples of that. So 2 times 100 is 200, 3 times would be 300, 4 times 400, and so on, 500, 600 and on and on and on. Harmonic Series is very important in music and we can think about the Hertz as representing our base frequency.

If we were to represent the low C in the image below then when we double that frequency we would be in the C an octave above. When we go three times that original frequency, we would be the G above that and if we went four times we would be the C above that and so we’re not always getting C’s. We’re getting different notes.

If we went from there we would get an E and we get a G and then a kind of B flat and so on and so forth. But there’s another way to think about pitch which is in terms of octaves and this is not a linear scale of 1 times, 2 times, 3 times, 4 times anymore. This is a scale of doubling every time. So 100, 200 Hertz, 400 Hertz, 800 Hertz, 1600 Hertz and so on and so forth.

If we go at those frequency ratios always doubling or rather than always multiplying by some integer multiple, we end up with successive octaves where they’re all Cs, from C to C to C to C and so you see we got C, we double it, we get the C the next octave up as seen below. We double that, we get the C the next octave up. We double that, we get to see the next octave up.

And so again, the way that we hear pitch, is not on this linear frequency scale, when there’s logarithmic octave scale because we hear these Cs as sharing something in common with each other and going from one C to the next is traversing this space of an octave even though the difference between one 100 and 200 Hertz and between 200 and 400 Hertz is different in Hertz space is 100 versus 200.

So again there’s this difference between how we represent things in frequency and how we hear them in terms of these octaves. This pitch, this logarithmic relationship. I want to go a little bit further than that because we hear something else that’s a little bit more complicated too when we’re listening to pitch instead of frequencies.

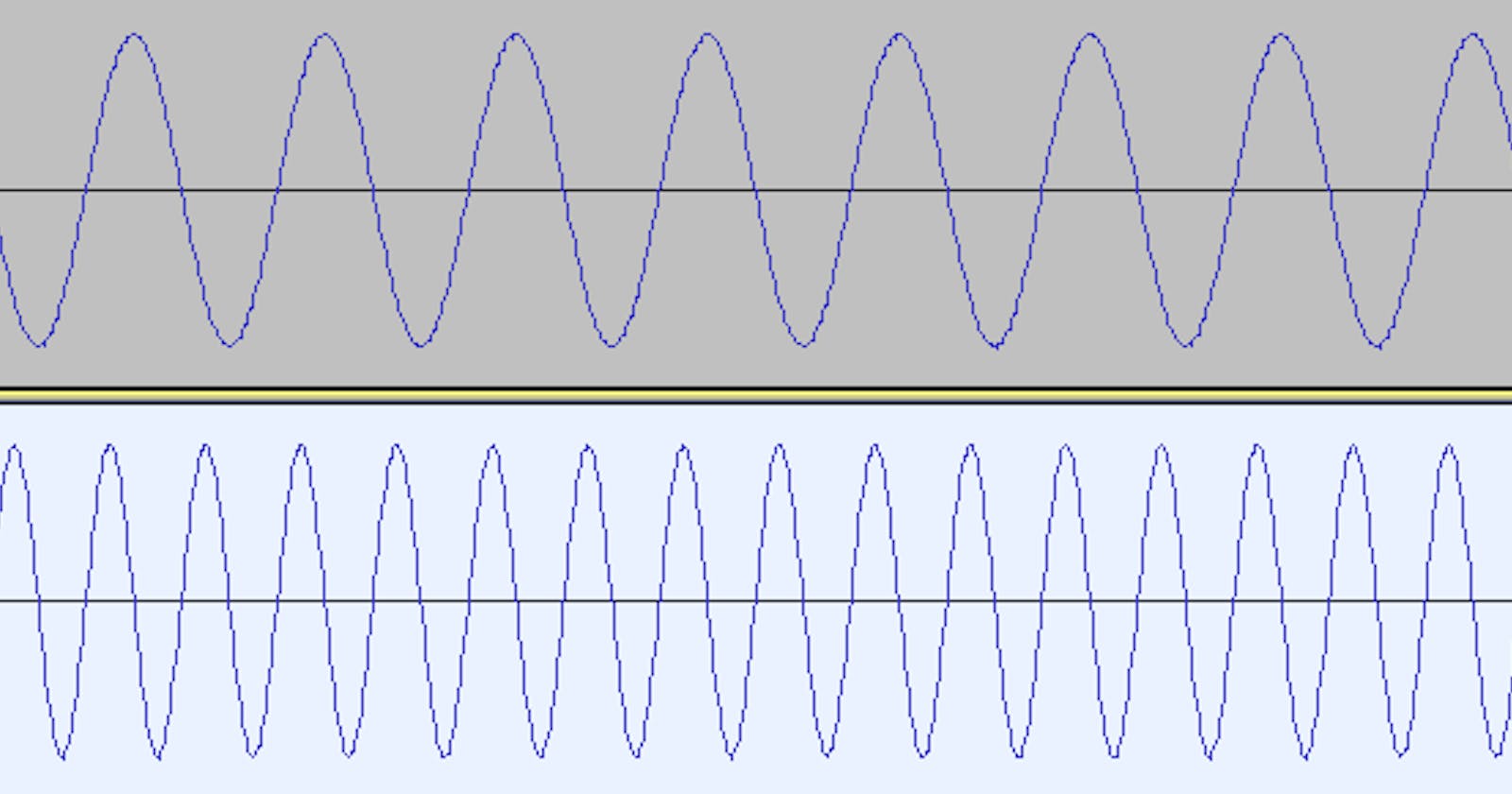
The image below contains two frequencies two sine waves, one is at 440 Hertz, the one on top, and then the one on the bottom is at 880 Hertz.

So there is a two to one relationships, they’re an octave apart from each other. Now what happens if we actually listen to them? That’s all for day 081. I hope you found this informative. Thank you for taking time out of your schedule and allowing me to be your guide on this journey. And until next time, be legendary.