Recap From Day 053

Day 053, we looked at working with time; how dynamic time warping works. We started by answering the question what if we take sequence B and shift it over just a bit to make a new sequence, D?

Today, we will continue from where we left off in day 053

Working with time

How Dynamic Time Warping Works continued

Dynamic time warping doesn’t only allow us to compute meaningful distance when one sequence is shifted earlier or later in time. Dynamic time warping also allows us to compute meaningful distances when the two sequences have different lengths in time. For example, the two sequences shown in the image below can also be warped to match quite closely.

Source

If we use dynamic time warping for gesture analysis, we often want this. After all, we could say that if this is the hand height in the air over time, we’re drawing almost exactly the same shape in both cases. We’re just moving more quickly in one example than the other.

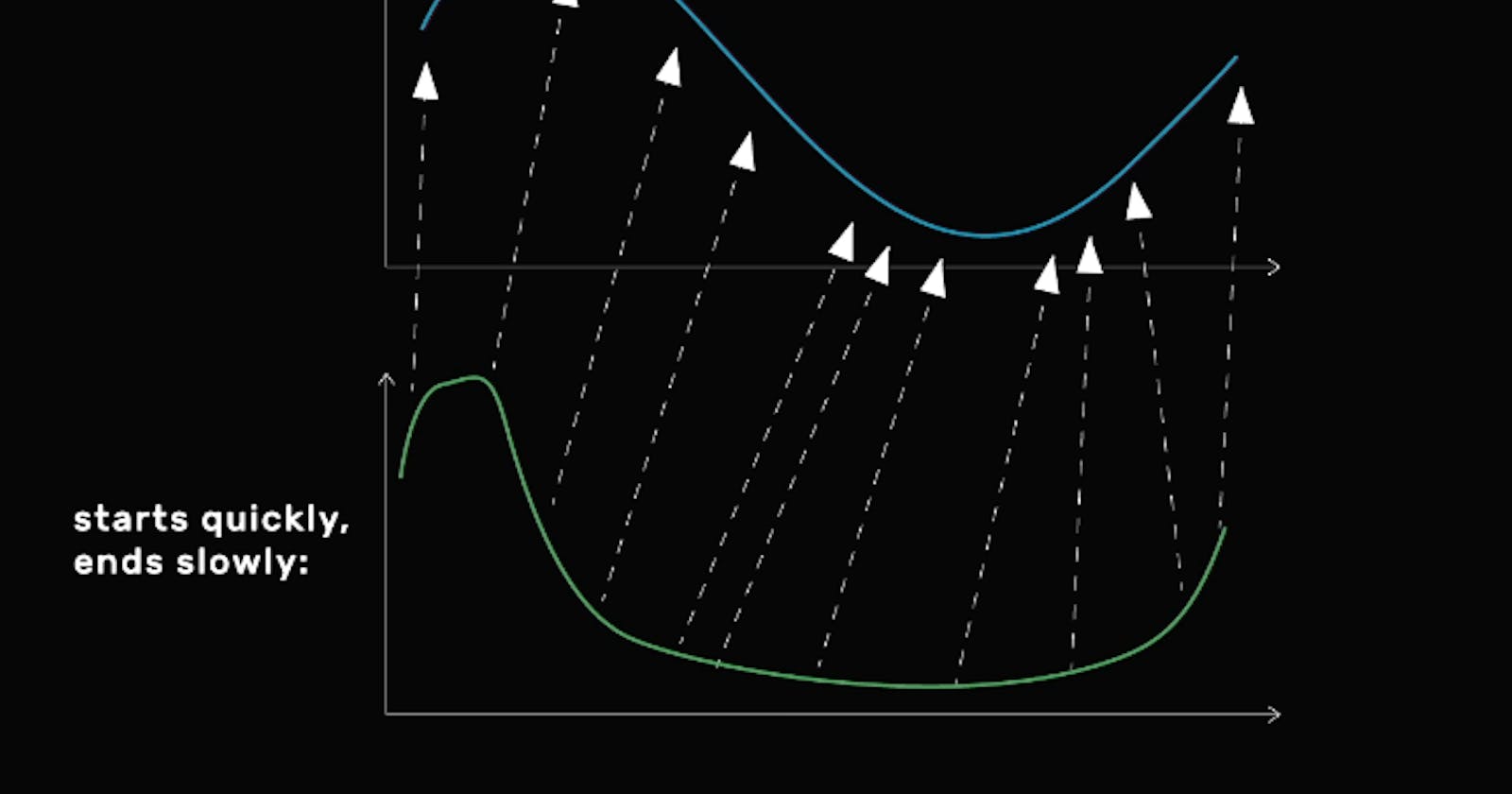
Dynamic time warping also allows us to compute meaningful distance when the speed with which movement through a sequence changes within the sequence. Say the hand motion started quickly and the finished slowly as shown below.

Source

Again, dynamic time warping can warp one of these gestures onto the other, where we can see that they are indeed almost exactly the same shape. So, how does dynamic time warping compute the best warping from one sequence to another? The basic approach is not too complicated, see a sketch below.

Say we have two sequences, A and B as shown below. Recall that warping sequence A to match sequence B can be understood as looking at each point in sequence A and finding a matching point in B. A good warp is one where each pair of points we’ve chosen to match are in fact close to each other, for instance, using Euclidean distance.

Source

Dynamic time warping requires that our first point in sequence A has to be matched to at least the first point in sequence B. It could also be matched to more points in sequence B if B starts out slower than A, but let’s ignore that for now. Dynamic time warping also requires that our final point in sequence A has to be matched to at least our final point in B as shown below.

Source

Within these two constraints, dynamic time warping works to find the warping but minimizes the overall distance between the two sequences. Dynamic time warping considers the best warping to be the warping that gives us the smallest distance, so it already will have computed the distance for us by the time it’s found the warping path.

So, dynamic time warping can be thought of as solving an optimization problem. That’s what we’ll look at tomorrow. That’s all for day 054. I hope you found this informative. Thank you for taking time out of your schedule and allowing me to be your guide on this journey. And until next time, be legendary.

Reference

*https://www.kadenze.com/courses/machine-learning-for-musicians-and-artists-v/sessions/working-with-time*