100 Days Of ML Code — Day 085
Recap From Day 084
Day 084, we looked at how we describe two sounds that actually have the exact same pitch and the exact same loudness but they sound really different from each other.
You can catch up using the link below. 100 Days Of ML Code — Day 084 Recap From Day 083medium.com
Today, we will continue from where we left off in day 084.
Fourier Theorem
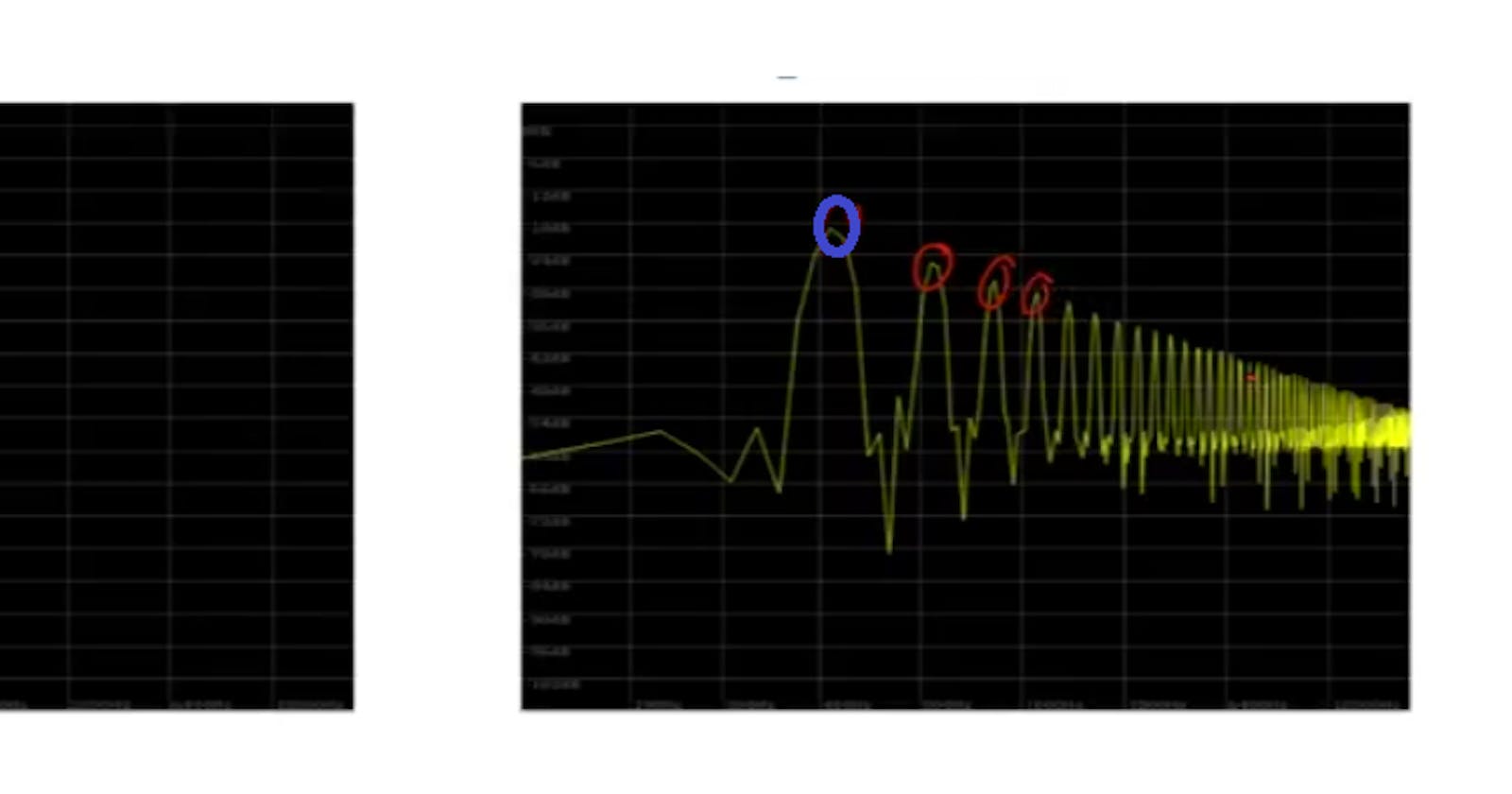
As seen in the image to the left below, we have a saw tooth wave, and so you see a number of peaks highlighted in red. So, you see a peak at 440 Hertz, and another one at 880, and at 1320 and 1760, and so on and so forth.

Those are all coming at integer multiples at the fundamental frequency 400. They’re at one times, two times, three times, four times 5 times, 6 times and on and on and on and you can notice each one is at lower decibels than the one that came before it. So our most energy is at 440 and then it goes down and down and down and down from there.
The recording above might be a little bit loud, so watch the volume on your headphones, or your speakers. It is a sawtooth wave, same frequency as the sine wave was but obviously, it has a very different timbre. And part of the way that we can explain this is because of the different spectra. Because they both have their peak at 440 Hertz (as highlighted in blue in the image below), but obviously there’s all this extra stuff happening in the different frequencies.

As we’ve seen before, we’re not hearing all those as separate sine waves or separate frequency components. They’re all kind of blending together to create this single sound in our minds and the way that we can understand this is through a very important theorem in music technology called the Fourier Theorem.
What the Fourier Theorem says is that “any periodic waveform can be represented as the sum of sine waves at frequencies that are integer multiples of a fundamental frequency” like our fundamental frequency in this case was 440 Hertz. In the integer multiples are what we saw before, 1 times 440, 2 times 440, 3 times 440, and so on and so forth.
What we’re looking at is at each of those integer multiples, we have a sine wave at some particular frequency, amplitude, and phase and if we add those together, we can represent any periodic wave form, like a sawtooth wave, or a triangle wave, or something like that.
Now it is important to emphasize the word periodic here. This is a very important caveat because in the real world, like waveform of a recording of someone talking, is not periodic, the cycles don’t repeat infinitely and infinitely and infinitely the way that sine wave would, or a sawtooth wave or something like that. So the Fourier Theorem only works for periodic wave forms.
That’s all for day 085. I hope you found this informative. Thank you for taking time out of your schedule and allowing me to be your guide on this journey. And until next time, be legendary.