Recap From Day 073
Day 073, we looked at the second part of designing custom algorithms for music. You can catch up using the link below. 100 Days Of ML Code — Day 073 Recap From Day 072medium.com
Today, we’ll continue from where we left off in day 073
Working with time
Designing custom algorithms for music
We saw from day 073 that particle filtering precisely has two critical features. Particle filtering can track nonlinear dynamics. To understand what is nonlinear dynamics of an object, imagine a car moving in a street observed through a video camera. Imagine that this car is accelerating and stopping more or less abruptly at different moment without apparent logic. Tracking this car can be difficult because it’s dynamic is complex. If the car were going straight, at a constant speed, it will be much easier. A tracking method such as particle filtering is flexible enough to adapt to complex dynamics such as the car’s ones and to be able to track it.
Another interesting feature of particle filtering is that it allows for non-Gaussian tracking. To understand what is non-Gaussianity we have to understand the Gaussian hypotheses. Imagine that we have to track a bird flying. This bird is going straight at a constant speed towards the wall in which there is only one circular hole of size twice the size of the bird. Using probabilities to track the position of the bird when it passes the wall is fairly easy. The probability is maximum at the center of the hole and quickly decreases for other possible positions near to the border of the wall and zero everywhere in the wall. In other words the bird is not silly and it’s more likely to pass where the danger is minimum, which is at the center of the hole, far from the borders.
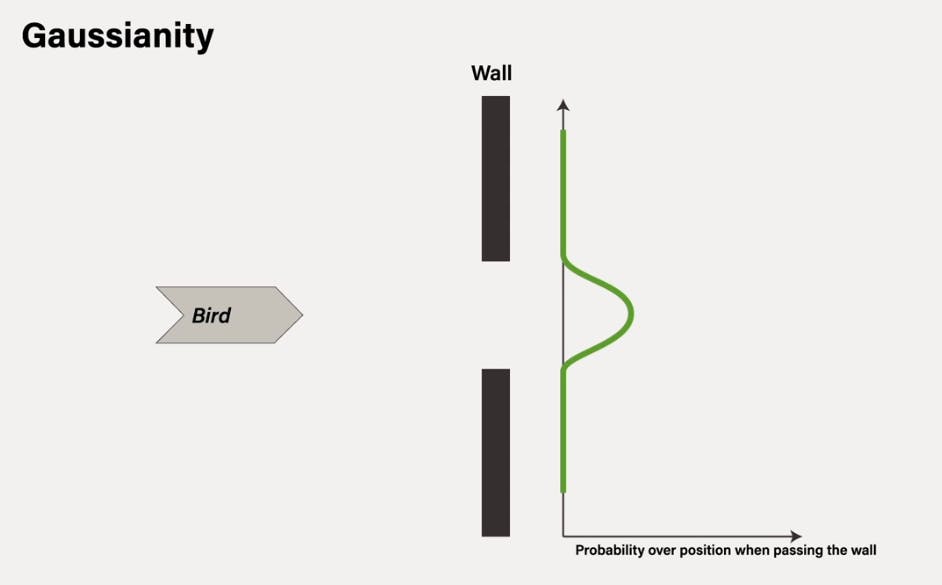
In this bird’s example, the tracking is Gaussian because the probability distribution over the positions of the bird has a bell shape with the maximum at the center of the hole, the bell mean. And then this decreasing as the position moves away from the mean.
In a non-Gaussian scenario, the probability distribution over the position of the bird is not a bell shape anymore. To illustrate such situation, imagine the same bird flying straight to the same wall in which they are now two holes instead of only one. In that case, the probability distribution may have the shape of two bell curves and not one.
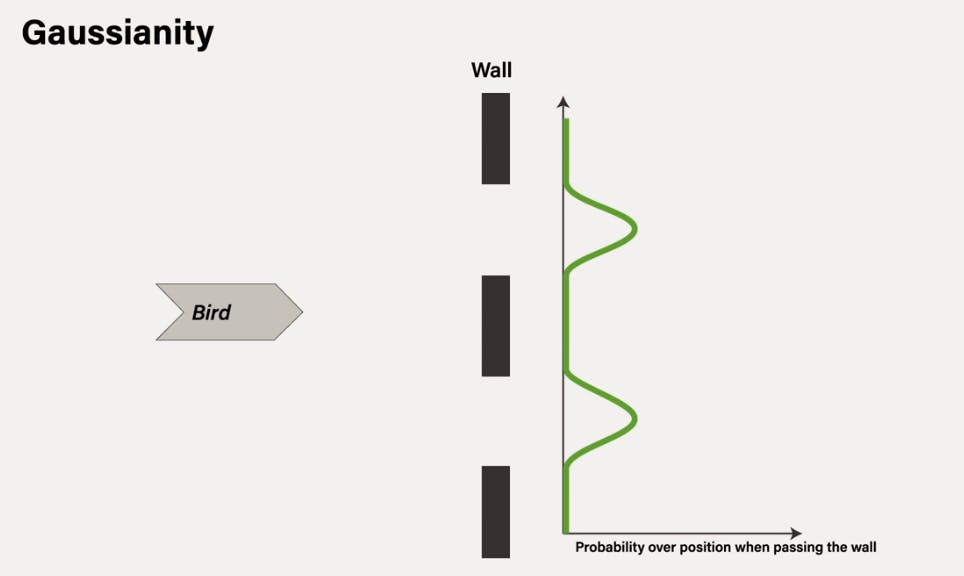
Such probability distribution is not Gaussian anymore. Here, it is actually the sum of two Gaussian distributions, but it is more complex than the single Gaussian. As a result, it’s slightly harder to track the bird passing the wall because we don’t know through which of the two holes the bird will choose to pass. And we have to keep both cases as possibilities.
GVF draws upon the features of particle filtering in order to track expressive variations in gesture execution. This technique is quite suitable for this problem because expressive gesture variations as the ones performed by musicians can have very complex dynamics highly nonlinear and can also have ambiguity or more complex probability distribution than Gaussian. In both cases, the need for having models that will offer new control for music drove changes and adaptation of conventional techniques. In the case of gesture follower, the need was to allow for real-time classification. In the case of gesture variation follower the need was to follow complex characteristics of the gesture.
That’s all for day 074. I hope you found this informative. Thank you for taking time out of your schedule and allowing me to be your guide on this journey. And until next time, be legendary.
References