Recap From Day 052

Day 052, we looked at working with time; how dynamic time warping works. We learned that with dynamic time warping we can compute the distance between two sequences of data with each data point consisting of several features.E.g X and Y values from a mouse, or pitch, or roll, and yaw values from a Wiimote, or even MFCCs from audio.

Today, we will continue from where we left off in day 052

Working with time

How Dynamic Time Warping Works continued

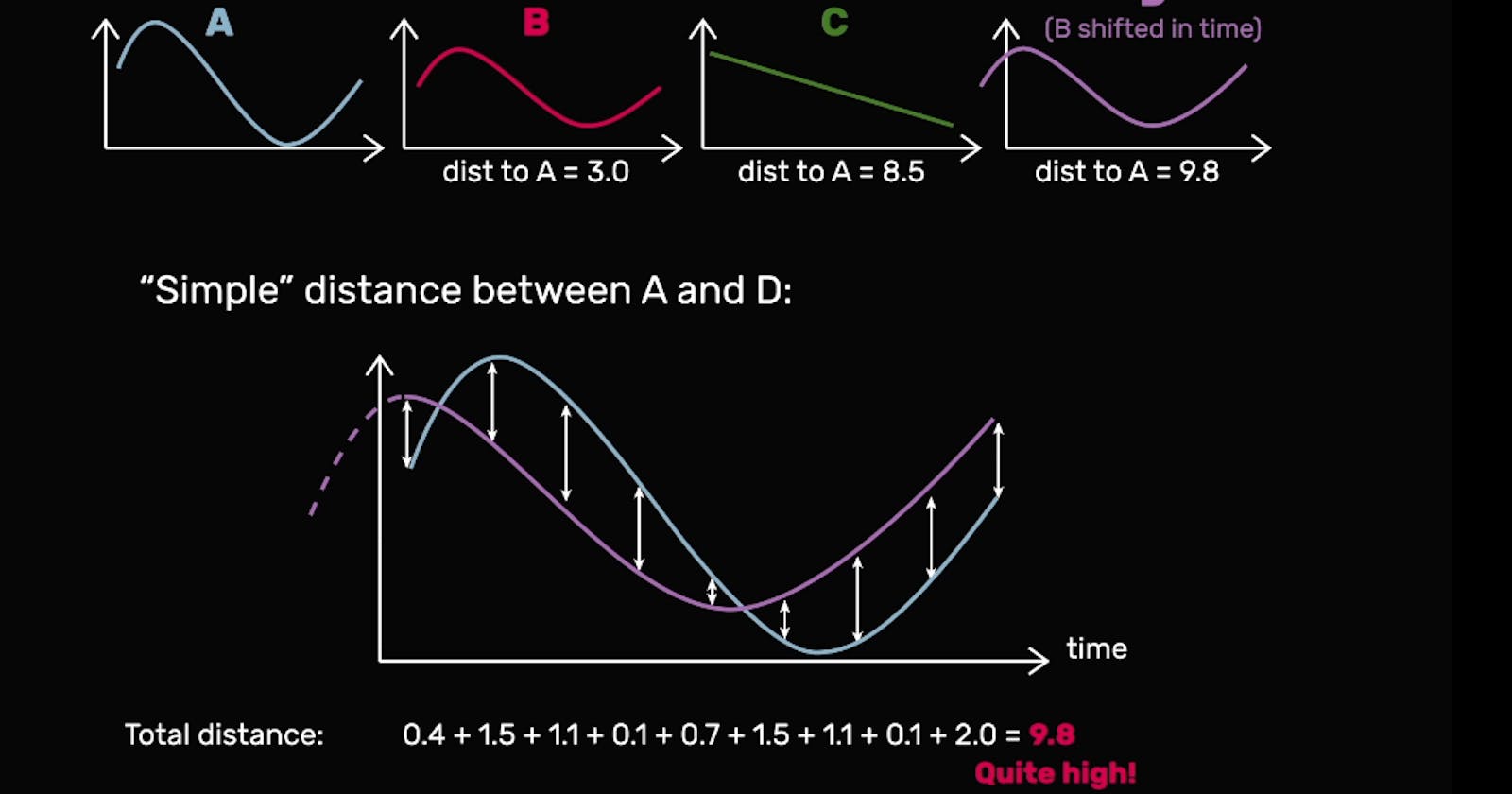
Let’s start by answering the question what if we take sequence B and shift it over just a bit to make a new sequence, D? This is equivalent to starting the hand wave a little bit earlier in B.

Source

What happens? Suddenly we see that our distance between the first point of A and D is much bigger, as it is for all the matching points, and if we add up all these distances, we see that the Euclidean distance between A and D is now bigger than the distance between A and C.

Source

If we use this distance to build a classifier using nearest neighbor and if A and C were our training examples, then we would find that D would be classified as belonging to the same class as C, not A, and this is one of the main problems with using Euclidean distance to compare sequences.

Two things that we would judge to be incredibly similar in shape will not be judged to be similar using Euclidean distance if they’re not aligned precisely in time. Dynamic time warping is a distance measure that accounts for the fact that sequences might shift a bit forward or backwards in time. It works by first computing the best way to warp one sequence onto another.

We can think of warping as taking each point in one sequence as shown in A in image below and optionally moving it forward or backward in time until the overall shape of the two sequence is the most similar as shown B in the image below.

Source

Equivalently, each point in the sequence we’ve warped is matched to at least one corresponding time point in the other sequence as shown below.

Source

Once we’ve aligned the sequences in the best way possible as shown below, we can then use Euclidean distance between pairs of matching points and sum these up just like we saw before to get an overall distance.

Source

Dynamic time warping will warp the sequence D to match the sequence A, as below. Before we compute the distance between them. The distance is now quite low, and if we compare the distance between D and A using dynamic time warping, we see that it is smaller than the distance between C and A and quite close to the distance between B and A.

Source

That’s all for day 053. I hope you found this informative. Thank you for taking time out of your schedule and allowing me to be your guide on this journey. And until next time, be legendary.

Reference

*https://www.kadenze.com/courses/machine-learning-for-musicians-and-artists-v/sessions/working-with-time*