Recap From Day 050
In day 050, we looked at working with time, dynamic time warping. We learned that With dynamic time warping we can detect when a specific gesture occurs even when we’re not using explicit segmentation with a button or something equivalent. Dynamic time warping will spot the fact we’ve just completed the gesture. In fact, this is sometimes called gesture spotting.
Today, we will continue from where we left off in day 050
Working with time
How Dynamic Time Warping Works
Now that we’ve seen what dynamic time warping can do from day 050, let’s take a peek at the algorithm itself. Dynamic time warping was designed specifically to compute the distance between two sequences of data.
Just like we’ve seen, each data point can consist of several features. Perhaps X and Y values from a mouse, or pitch, or roll, and yaw values from a Wiimote, or even MFCCs from audio.
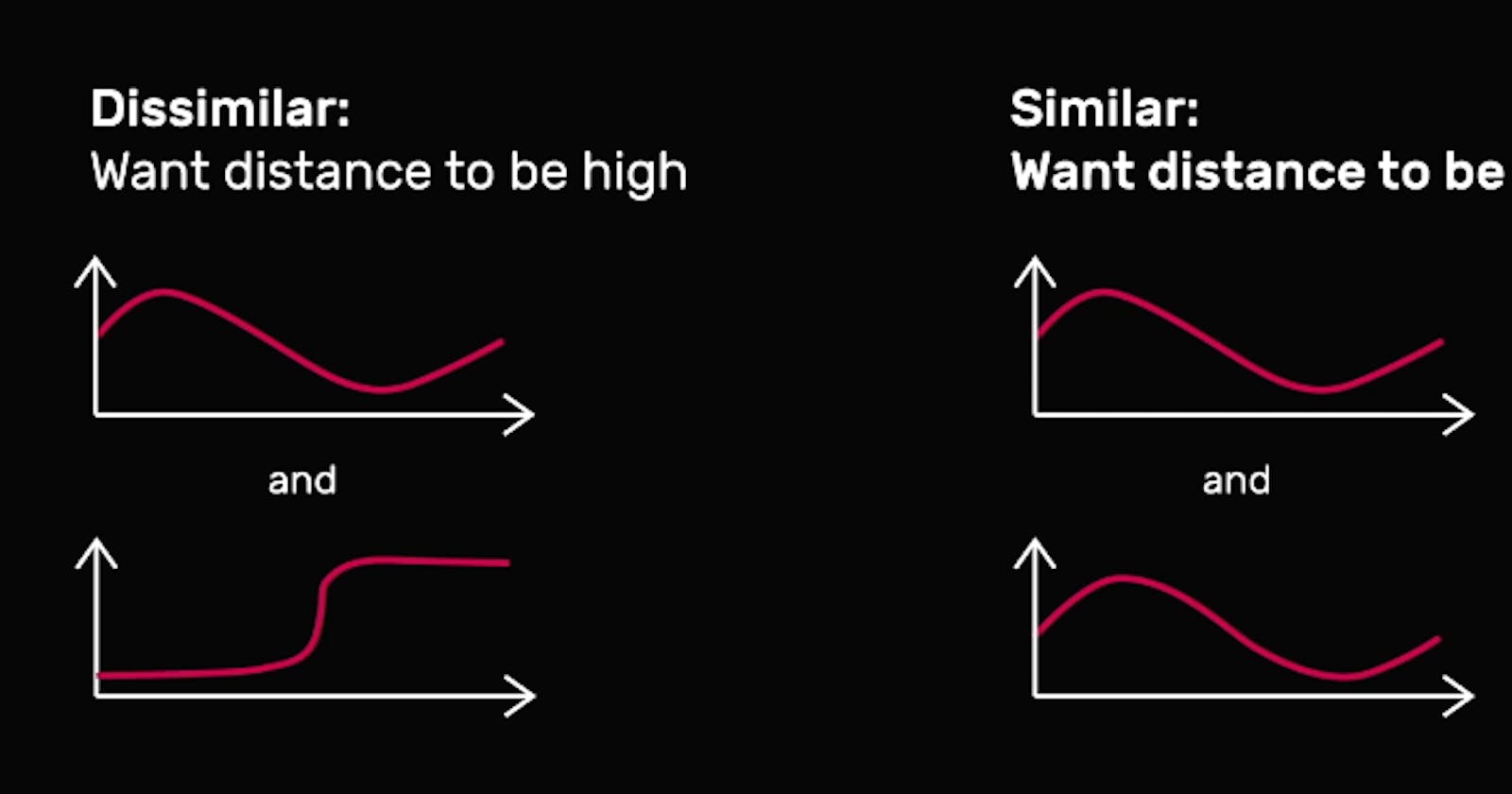
So if we wanted to design a good distance metric that is high when two sequences are dissimilar and low when two sequences are similar, how could we go about that?
We’ve already seen one distance function in detail, Euclidean distance, so let’s start there. As we discussed some days ago, Euclidean distance is often a natural distance measure to use between two objects in the physical world.
If we have two points on a plane, Euclidean distance is simply the length of the line we draw between them, and in this two-dimensional space, we can derive a formula for the length of that line using the Pythagorean theorem.
We can do the same thing to measure the distance between two objects in the three dimensional world, and we can even generalize this definition to cover an arbitrary number of dimensions.
As we’ve seen, the equation above is what is used by our nearest neighbor algorithm to compute the distance between examples in feature space if we have some number of features N.
That's all for day 051. I hope you found this informative. Thank you for taking time out of your schedule and allowing me to be your guide on this journey. And until next time, be legendary.
Reference

](https://cdn-images-1.medium.com/max/2000/1*7Gu3SgLYDCx1x4G5LDqK7A.png)
](https://cdn-images-1.medium.com/max/2000/1*AAqmOk9GbU7s9C5XSOCklA.png)