Recap From Day 032
In day 032, we looked at working with audio input: Common audio features. We saw that the RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or the square of the function that defines the continuous waveform.
Today, we’ll continue from where we left off in day 032.
Working With Audio Input: Common Audio Features Continued
Fast Fourier Transform (FFT)
“A fast Fourier transform (FFT) is an algorithm that samples a signal over a period of time (or space) and divides it into its frequency components. These components are single sinusoidal oscillations at distinct frequencies each with their own amplitude and phase.”
Let’s look at a relatively simple audio feature that uses the Fast Fourier transform (FFT). If you are interested in audio and you don’t know about the FFT, I highly recommend you go and learn about it. You can start with the Audio Signal Processing for Music Applications course on Coursera, created by Universitat Pompeu Fabra of Barcelona, Stanford University. Audio Signal Processing for Music Applications | Coursera About this course: In this course you will learn about audio signal processing methodologies that are specific for…coursera.org
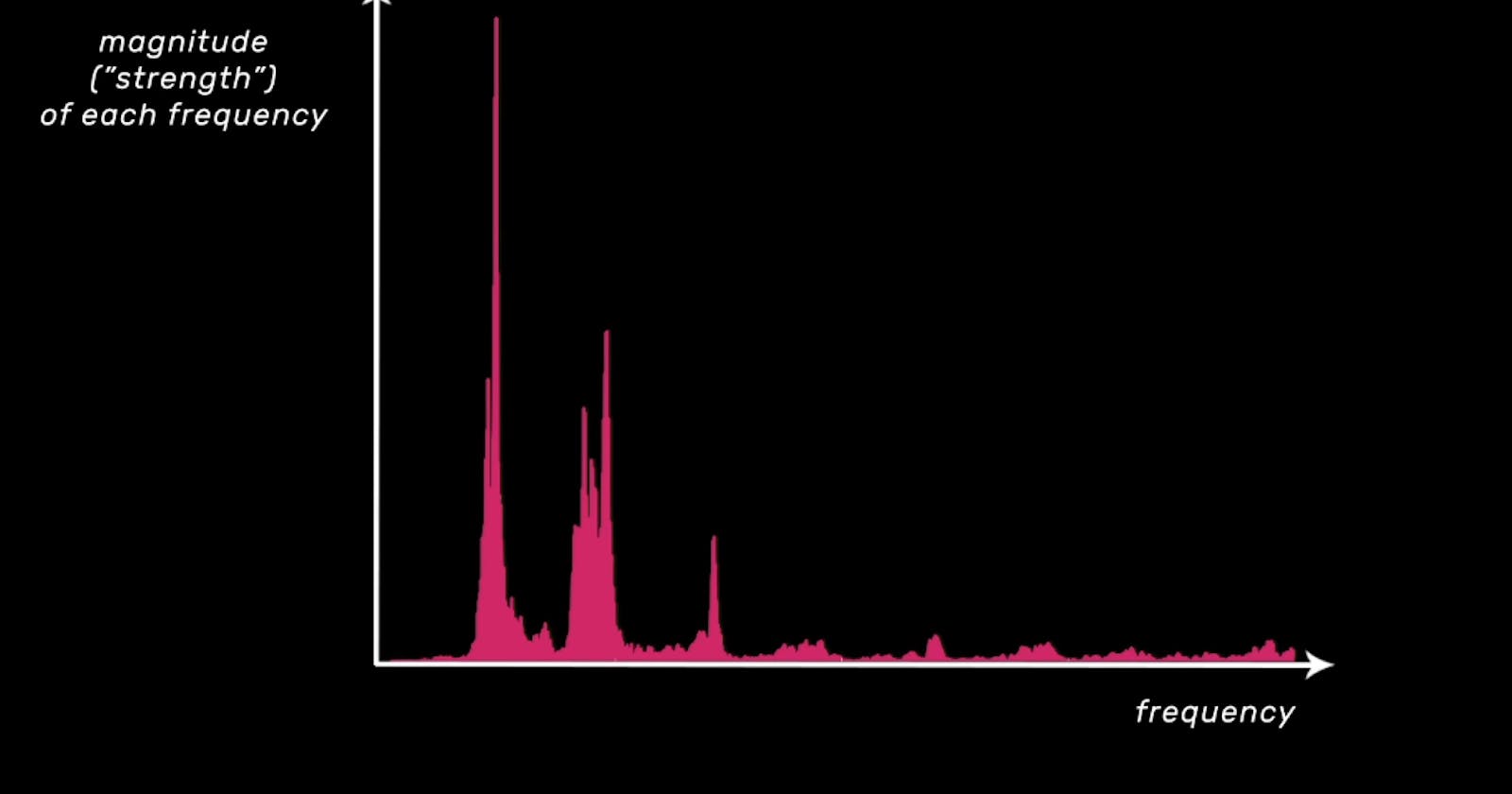
The diagram below shows how the FFT is usually plotted, with frequency from low to high along the x-axis, and the magnitude, or strength, of each frequency along the y-axis.
Depending on how long our analysis window is, our FFT will give us a different number of frequency magnitude values. This typically ranges from 16 or 32 values at minimum, to maybe 4,096 at maximum. We could actually use a whole list of FFT magnitude as our feature vector, and try to get the computer to learn something from it.
For relatively constraint sets of inputs sounds, we’ll be able to build a decent pitch classifier or maybe timbre classifier using just the FFT magnitude values. But if we want to make sure that every feature we use is relevant and informative, while also avoiding having a huge number of features, we can often do better than just the raw FFT.
One simple thing we can do is identify the one frequency in the sound that has the single highest magnitude. If we want to build a very simple pitch classifier, for instance, to track the pitch of a single instrument, where out instrument, microphone placement and acoustic environment aren’t changing so much, this might give us some information that we could use. Certainly, this will be enough to give us information about whether our instrument is playing a low note or a high note, and it might be one useful feature among several for other types of tasks. For instance, classifying whether someone speaking is male or female.
It’s good to know that you’re still here. We’ve come to the end of day 033. I hope you found this informative. Thank you for taking time out of your schedule and allowing me to be your guide on this journey. And until next time, remain legendary.
Reference

](https://cdn-images-1.medium.com/max/2118/1*Ga7qWXx0K_mNWtWEmoRHQQ.png)